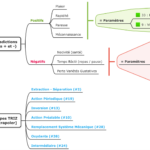
Après avoir synthétisé une contradiction technique, il reste à (tenter de) la résoudre à l’aide de la matrice TRIZ, ressource disponible en format classique (PDF) ou en ligne.
Rappel ou précision : cette matrice concentre, aux intersections de 39 paramètres, les fameux 40 principes inventifs destinés à dissoudre des contradictions techniques – des demandes antagoniques portant sur des aspect différents. Un exemple et cas fréquent : un surcroît de puissance (effet désiré) est souvent accompagné par une consommation d’énergie supplémentaire (effet indésirable).
Les quatre stades du processus se calquent très bien sur le schéma figurant la philosophie TRIZ :
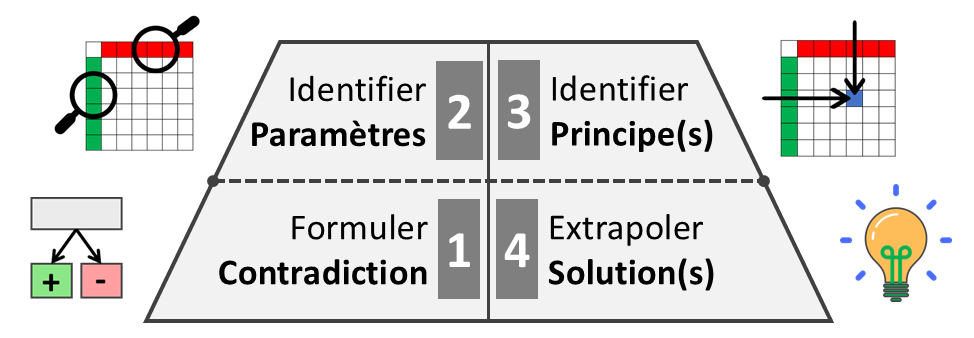
Les quatre stades en étant un peu plus explicite :
[1] Définir le problème
Cerner la contradiction en isolant la source (ou le système), l’effet positif (ce que l’on veut obtenir ou préserver) et l’effet négatif (ce qu’il faut éviter ou éliminer). Pas de doctrine absolue pour ce faire, l’une ou l’autre pratique est recevable.
[2] Identifier les (des) paramètres en opposition
Pour et avant d’entrer dans le corps de la matrice, il faut identifier au moins une paire de paramètres. En abscisse (horizontale), le paramètre correspondant à l’effet négatif et, en ordonnée (verticale), le paramètre évoquant l’effet positif.
Les 39 paramètres étant (très) génériques, il ne faut pas se priver d’en sélectionner plusieurs ; en fait, tout paramètre qui semble coller au problème mérite d’être pris en compte.
[3] Relever les principes aux intersections
Hormis quelques cas particuliers, le croisement de deux paramètres (un effet positif en ordonnée X un effet négatif en abscisse) livre jusqu’à quatre principes inventifs, classés par ordre de probabilité (d’adéquation ou de solution) décroissante.
A ce stade, il s’agit de prendre note des solutions génériques aux intersections (matrice TRIZ) des paramètres identifiés au stade précédent.
[4] Extrapoler une (ou plusieurs) solution(s)
Place à l’imagination pratique et créative car, à l’instar des 39 paramètres, les principes inventifs sont des principes génériques. Il faut maintenant interpréter ou extrapoler les principes identifiés à l’issue de l’étape précédente – s’en servir comme tremplin ou comme boussole – afin de concrétiser une solution (voire même plusieurs) au problème en question.
NB : pour bien ou mieux exploiter les principes-candidats, tout est bon à prendre : l’intitulé, les déclinaisons et les exemples (cf. répertoire principes).
Itération(s) en option !
Aucun résultat satisfaisant après un premier tour de piste ? Il n’est pas sot d’en refaire un second en remettant en question la formulation de la contradiction. C’est souvent à cette étape que le bas blesse.
On reprend cette fois avec un cas pratique ?